¡Inecuaciones!

Las inecuaciones son desigualdades algebraicas en la que sus dos miembros se relacionan por uno de estos signos:

<	menor que	2x − 1 < 7
≤	menor o igual que	2x − 1 ≤ 7
>	mayor que	2x − 1 > 7
≥	mayor o igual que	2x − 1 ≥ 7

La solución de una inecuación es el conjunto de valores de la variable que la verifica. Se expresa mediante: Una representación gráfica. Un intervalo.

Ejemplos:  2x − 1 < 7

2x < 8     x < 4

(-∞, 4)

2x − 1 ≤ 7

2x ≤ 8     x ≤ 4

(-∞, 4]

2x − 1 > 7

2x > 8     x > 4

Si a los dos miembros de una inecuación se les suma o se les resta un mismo número, la inecuación resultante es equivalente a la dada.

3x + 4 < 5    3x + 4 − 4 < 5 − 4    3x < 1

Si a los dos miembros de una inecuación se les multiplica o divide por un mismo número positivo, la inecuación resultante es equivalente a la dada.

2x < 6    2x : 2 < 6 : 2    x < 3

Si a los dos miembros de una inecuación se les multiplica o divide por un mismo número negativo, la inecuación resultante cambia de sentido y es equivalente a la dada.

−x < 5    (−x) · (−1) > 5 · (−1)   x > −5

1 Quitar corchetes y paréntesis.

2 Quitar denominadores.

3 Agrupar los términos en x a un lado de la desigualdad y los términos independientes en el otro.

4 Efectuar las operaciones

5 Si el coeficiente de la x es negativo multiplicamos por −1, por lo que cambiará el sentido de la desigualdad.

6 Despejamos la incógnita.

7 Expresar la solución de forma gráfica y con un intervalo.

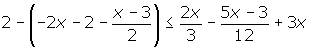
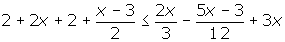
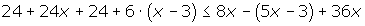
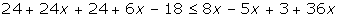
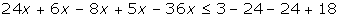
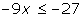
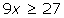
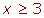
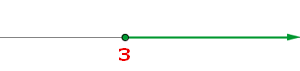
[3, +∞)

ESTO ES UN POCO DE LO QUE SERIAN LAS INECUACIONES, ESPERAMOS QUE LES HAYA SERVIDO Y NOS VEMOS EN LA PRÓXIMA ENTRADA!!